 |
| |
A Colorful Journey through Endless Patterns of Quick Wits |
|
|
|
|
|
|
|
Home /
History /
Two Oval
Stools to a Table |
|
|
|
|
|
|
|
Centuries of the Ovals |
This well-known, classic puzzle
with transformation of two oval stools into a circular
table top has long and interesting history. More than
180 years ago, in 1821, John Jackson posed in his book
Rational Amusement for Winter Evenings a puzzle how to
transform a circle into two hollow ovals as shown below, and
proposed an 8-piece solution. Could you discover how it
can be done?
|
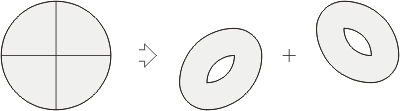 |
Jackson’s Table & Oval Stools puzzle.
|
|
|
Then, at the beginning of the 20th
century this puzzle attracted attention of Sam Loyd, who
was the greatest America's puzzle creator. In Loyd's
legendary Cyclopedia of 5000 Puzzles, Tricks &
Conundrums, the puzzle was posed under the name "An
Old Saw with New Teeth" as a challenge how to dissect
two ovals with an oval hand hole in each of them into
the fewest number of parts which can form a circular
table top.
|
 |
Loyd's "An Old Saw with New Teeth" puzzle as it appeared
in his Cyclopedia of 5000 Puzzles, Tricks &
Conundrums.
|
|
|
Loyd published it as a contest,
showing then a better, 6-piece solution which was based
on a famous Great Chinese Monad pattern. Try to find
that 6-piece solution using as a hint that pattern and
patterns depicted on two ovals and on the resulting
circle as shown in in the illustration below. Keep in
mind that diagrams shown in the illustration contain all
necessary lines to make your cuts, but not every of
these lines you will need to use, though.
|
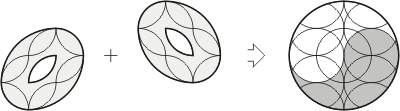 |
Pattern for 6-piece solution based on the Great Chinese
Monad.
|
In 1997
Greg Frederickson,
the World's biggest expert in dissection puzzles,
published an outstanding book on history and
achievements in this old and comprehensive field of
recreational math -
Dissections: Plane & Fancy.
Chapter 15 in that book is fully devoted to dissections
with curved figures, and also describes the above and
some other variations of the puzzle with two hollow
ovals. In the book Greg shows quite different, novel
6-piece solution to Jackson's ovals.
Since the first publication of Jackson's puzzle there
were numerous attempts to improve the 6-piece solution
to the puzzle. Finally, in March of 2004 I was lucky to
discover several new 6-piece solutions, two basic
solutions containing just five(!) pieces each, more than
a dozen of different modifications of these basic
5-piece solutions, and proofs that in math sense there
is an infinite number of 5-piece solutions. In every of
them one piece is flipped over. Finding any of 5-piece
solutions is not an easy task, so try to discover one of
the simplest of them. Could you do this? Hint. The
diagrams below contain all necessary lines to make your
cuts. Of course, not all of them are needed to be used
for this. And keep in mind that in a 5-piece solution
one piece is allowed to be flipped over.
|
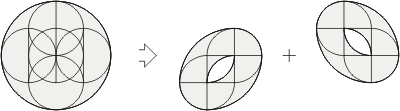 |
Diagram for 5-piece solution.
|
Last but not least, there is a
variation of the hollow-ovals-to-circle puzzle posed by
Sam Loyd in his attempts to find solution with the least
number of pieces. It also is based on the Great Chinese
Monad pattern described above, and you can easily solve
it keeping in mind that every oval is divided in exactly
two the same pieces. The illustration below shows this
Loyd's variation and all necessary lines to make you
cuts. Again, please remember that you will need just
some of these lines to cut both ovals.
|
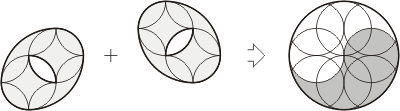 |
Loyd’s variation with four pieces.
|
|
|
|
|
|
|
|
Notes & References |
|
|
|
|
|
|
| |
|
|
|
|
|
Last
Updated: December 3, 2009
Posted: August 30, 2005 |
|
|
|
|
|
|
|
|
|
