|
Home /
Publications
/
Puzzle Classics at G4G7 -- Solutions |
|
|
|
Puzzle Classics at G4G7 --
Solutions |
 |
|
|
|
|
Solutions shown below were found by
the authors of the respective puzzles, unless otherwise
is stated. For some challenges there can be more than
one solution.
Write
us if you can improve any of the shown results. |
|
|
|
|
|
|
|
Puzzleland Gingerbread |
Three solutions to the three challenges
of Loyd’s
Puzzleland Gingerbread puzzle are shown below.
|
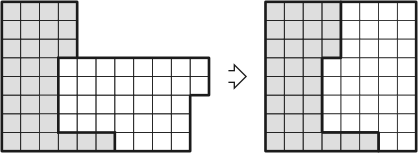 |
The solution by Sam Loyd to
Challenge 1.
|
|
|
|
|
 |
The solution by Martin Gardner
to Challenge 2. |
|
|
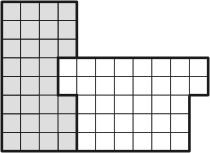 |
The solution by Serhiy
Grabarchuk
to Challenge 3. |
|
|
|
|
|
|
|
|
A Card Puzzle |
The original solution to Challenge
1, and solutions to Challenges 2 and 3 are shown in the
illustrations below.
|
|
|
The original solution to
Hoffmann's Card puzzle as it appeared in his book
Puzzles Old & New,
at left; its reconstruction, at right.
|
|
|
|
|
 |
The solution to Challenge 2. |
|
|
 |
The solution to Challenge 3. |
|
|
|
|
|
|
|
|
Out of the Y |
A 2-matchstick solution to the
classic Olive & Glass matchstick puzzle, and a 5-move
solution to the Out of the Y coin puzzle are shown below.
|
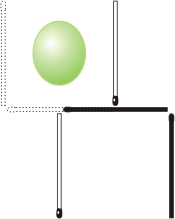 |
2-matchstick solution to the Olive & Glass puzzle.
|
|
|
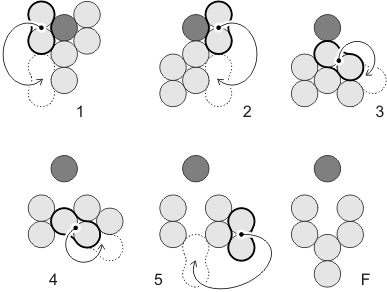 |
5-move solution by Serhiy
Grabarchuk, Jr. to the Out of the Y puzzle. |
|
|
|
|
|
|
|
Classic Tangram |
|
The solutions to the four proposed
shapes assembled of all the seven pieces of the classic
Tangram each are shown below. |
 |
The four shapes assembled
using all the seven pieces of the classic Tangram each
time. |
|
|
|
|
|
|
|
The Tangramboard |
The solutions to the four proposed
shapes assembled of all the seven pieces of the
Tangramboard each are shown below.
|
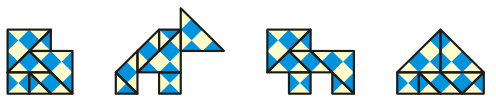 |
The four shapes assembled
using all the seven pieces of the Tangramboard each time. |
|
|
|
|
|
|
|
The Contour Tangram |
The solutions to the four proposed
shapes assembled of all the seven pieces of the Contour
Tangram each are shown below.
|
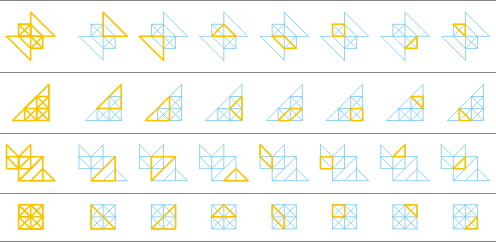 |
The four shapes assembled
using all the seven pieces of the Contour Tangram each
time. |
|
|
|
|
|
|
|
Tangram Battleship |
The diagram below shows exact
positions of all the seven Tangram ships on the board.
|
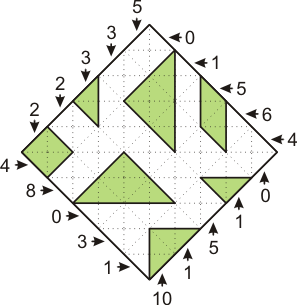 |
The solution to the Tangram
Battleship challenge. |
|
|
|
|
|
|
|
Tangram Packing |
The 3D diagram below shows the exact
positions of all the seven Tangram pieces in the chain
placed within a 2x2x2 cube. The asterisk (*) shows the
contact of two end triangles where the chain is closed
in a loop.
|
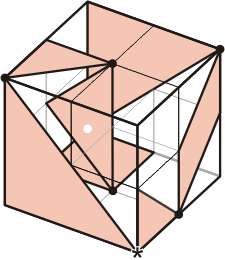 |
The Tangram Chain running
within a 2x2x2 cube. |
|
|
|
|
|
|
|
TanFrames: Squaring |
The diagrams below show how all the seven Tangram pieces form six fully closed square outlines.
|
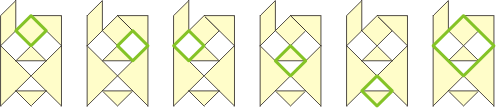 |
All the seven Tangram
pieces can form six square outlines. |
|
|
|
|
|
|
|
Uniline Tangram: T-Unicursal |
How to form the unicursal T-shape
using all the seven pieces of the classic Tangram is
shown in the diagrams below.
|
 |
The unicursal Tangram
T-shape, at left; how to draw it with one line, at
right. |
|
|
|
|
|
|
|
The Diamond Puzzle |
The solutions to the original
square and four proposed shapes assembled of all the ten
pieces of the Diamond Puzzle each, and a small square
assembled of four pieces of the puzzle are shown below.
|

 |
The original square
assembled of all the ten pieces of the Diamond Puzzle.
|
|
|
 |
The four shapes assembled
using all the ten pieces of the Diamond Puzzle each
time.
|
|
|
 |
A small square assembled of
a subset of four pieces of the Diamond Puzzle. |
|
|
|
|
|
|
|
Martha's Vineyard |
During the Ukrainian puzzle
championship mentioned in the article, a maximal known
solution with 46 vines (see the diagram below) was discovered independently by
several solvers from Russia and Ukraine: Olga Leontieva, Andrey German, Andrey
Khodulyov, Mikhail Khotiner, Alexei Chaplyun, and Anton
Volchyk. Bear in mind that vines are
considered as mathematical points, and in the diagram
they are enlarged in order to show the solution clearly.
|
 |
46-vine solution to Loyd’s
“Martha’s Vineyard” puzzle. |
|
|
|
|
|
|
|
The Two Ovals-to-Table Story |
Three solutions to the three challenges
of the Two Ovals-to-Table puzzle are shown below.
|
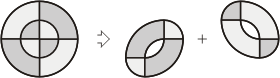 |
8-piece solution by John
Jackson, 1821.
|
|
|
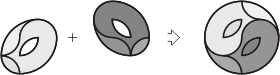 |
6-piece solution by Sam
Loyd, 1901.
|
|
|
 |
5-piece solution by Serhiy
Grabarchuk, 2004. |
|
|
|
|
|
|
|
|
|
|
| |
