 |
| |
A Colorful Journey through Endless Patterns of Quick Wits |
|
|
|
|
|
|
|
Home /
Publications
/
Puzzle Classics at G4G7 |
|
|
|
|
|
|
Classic puzzles make a substantial
and distinctive part within all puzzles available to
puzzlers in different forms, real and virtual. Many of
them are well-known, and still they hide a lot of
surprises which can lead puzzlers to new and improved
solutions, while puzzle creators can come up with new
challenges and variations. Below I'd like to describe
several classic puzzles for which new challenges and
improved solutions were found in several past years. They
are presented in seven puzzle themes, and I
will start with a very simple puzzle.
-----
Important:
All puzzles are published here with the kind permission
of their authors, where applicable. Copyright to all
presented puzzles stays with their respective
authors, unless otherwise is stated.
----- |
|
 |
Printable Puzzle: To
solve some of the puzzles which will be described below you
can print their pieces/grids. For this, click the respective
image marked with the pictogram shown at left to go to a new window with the puzzle pieces; then you
can print them and (when necessary) cut them out. Note that all these puzzles
are copyrighted, so you can print them for your own use only,
and not for any kind of commercial profit. |
|
 |
Play Puzzle: Click
an image marked with the pictogram shown at left to go
to a page with an interactive version of the respective
puzzle. |
|
|
|
|
|
|
Theme A: Sweet Dissection |
|
|
|
Puzzleland Gingerbread |
This Sam Loyd's puzzle has two
tasks in it. In the first you have to cut the cake into
two parts which can make a square. Can you find how it
can be done?
Also, Loyd gives a second challenge to the puzzle, but,
as Martin Gardner writes in his comments to this puzzle,
because of the incompleteness of the text it's not clear
what the problem is, and his guess is that Loyd asks his
readers to divide the cake into two largest possible
congruent pieces. Try to find these pieces.
Now there is a third challenge to this little puzzle.
Understanding children as creative puzzle persons we can
also suppose that Loyd's second puzzle could be interpreted in
the next way: "Divide the whole gingerbread into two
parts each of which is self-symmetric." Can you solve
this challenge as well?
Note that in the first and third challenges you should
use the whole gingerbread with no part left over. |
  |
The “Puzzleland
Gingerbread" puzzle as it appeared in Loyd’s
Cyclopedia of 5000 Puzzles, Tricks & Conundrums.
|
|
|
|
Theme B: New Card Assembling |
|
|
|
A Card Puzzle2 |
More than a century ago (in 1893)
Professor Louis Hoffmann published this tiny puzzle in
his classic collection, Puzzles Old & New. You have four
simple cards, all are fives. His original challenge was
to assemble cards, face upward, so that each of them
shows only four of their pips. How can you do that?
We with my sons have added to the challenge two new
ones which use the same set of four cards. One challenge
is to assemble the cards so that to get each of them to
show only three of their pips.
Another challenge is to form some shape of these four
cards so that one of them shows just one pip, another
shows two pips, the third one -- three pips, and the
last one shows four of its pips.
|
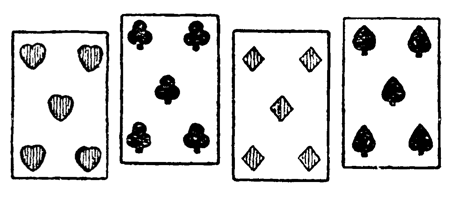  |
Professor Louis Hoffmann’s
set of four cards from his
book Hoffmann's Puzzles Old & New.
|
|
|
|
|
|
Theme C: Coin Cleaning |
|
|
|
Out of the Y3 |
A very popular matchstick puzzle
"Olive & Glass" shown below at left is a true puzzle
classic. The object is to move exactly two matchsticks
so that the glass remains the same (though in other
position), but the olive is out of the glass. Can you
find out how to perform this?
Our family puzzle "Out of the Y" is a modern version of
the Olive & Glass puzzle, but instead of matchsticks it
uses coins which form "glass and olive" as shown in the
illustration below right. Moving a pair of adjacent
coins at a time, reassemble the Y (keeping its exact
form) in other place so that the central coin (shown in
dark) is out of the Y. "Out" means that it will not
touch to the Y at all. Could you perform this in five
pair-moves? Note that the Y in its new position may have
other orientation than that initial.
Pairs must be moved without rotating; see small sample
diagrams beneath the Y. After each move you must form at
least one coin triplet which includes one/two coins
which were just moved and two/one coins from among those
unmoved. Coins in such a triplet must form some
triangle. Note that you are not allowed to move the
central (dark) coin!
|
 |
The Classic Olive & Glass Puzzle. |
|
|
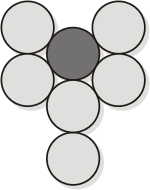 |
Out of the Y by Grabarchuk Family. |
|
 |
|
|
|
|
|
|
|
|
|
Theme D: The Tangram Puzzle Family |
|
|
The old good Tangram is so
well-known that it's quite impossible not to try it in
different variations. I'd like to show some different
puzzles created and developed by me and my sons within this theme.
|
|
|
|
|
|
Classic Tangram |
|
This puzzle is a square divided into seven pieces as
shown at left. It's an assembling puzzle, so using all
the seven pieces you can form a huge number of different
shapes as those shown below. Pieces
can be rotated and flipped over, but not overlapped.
Can you assemble them? |
|
|
|

|
Some shapes assembled using
all the seven pieces of the classic Tangram.
|
|
|
  |
The Tangramboard by Serhiy Grabarchuk. |
|
|
|
The Tangramboard4 |
|
In this puzzle the classic Tangram
pattern is merged with a 4x4 checkerboard. This gives
seven checkered pieces; the pieces are one-sided.
The object is to assemble
different regularly checkered shapes. Some patterns
possible to create with this set are shown below. How
they can be assembled? Keep in mind that pieces are
one-sided, and they can be rotated, but not flipped
over or overlapped. The fact that pieces are patterned
and one-sided add to the Tangramboard challenges
and the solving process a totally new logic. You can
also play the extended version of this puzzle,
The Tangramboard Plus. |
|
|
|

|
Some shapes assembled using
all the seven pieces of the Tangramboard.
|
|
|
  |
The Contour Tangram by Serhiy Grabarchuk. |
|
|
|
The Contour Tangram |
|
This puzzle consists of seven
transparent pieces with thin outlines; you can easy
imagine them as done of a thin wire. You can use this
set just like a traditional assembling puzzle making
different shapes, but unlike a classic Tangram they can
be overlapped, partially or in full, so that they can
make several layers. At the following
page you can see and play with an interactive Flash
version of this puzzle. The page presents about two
dozen different shapes to play with. Of course, there
are much more interesting shapes which use this set. |
|
|
|
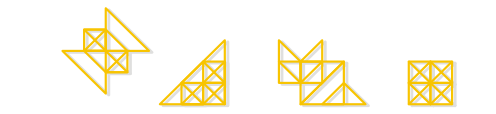
|
Some shapes assembled using
all the seven pieces of the Contour Tangram.
|
|
|
|
Tangram Battleship5 |
This is a paper-n-pencil puzzle
which uses the whole set of Tangram pieces as elements
of a battleship type of puzzles. On the board shown
below find exact positions for all the seven Tans; they
are shown next to the board, at right. Outlines of all
the Tans should exactly and fully coincide with some
lines of the board's grid. Each number (with its arrow)
around the board shows how many small single triangles
lie in the corresponding row or column. You can rotate
and flip pieces over, but no two of them can overlap or
touch each other, even at a corner..
|
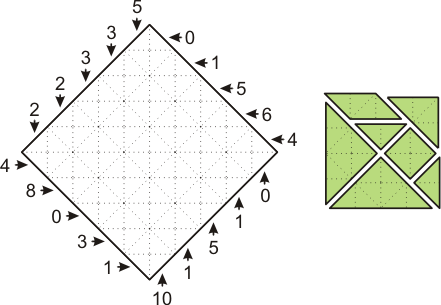 
|
Tangram Battleship by
Serhiy Grabarchuk.
Put all the seven Tangram ships on the grid according to
the numbers around it.
|
|
|
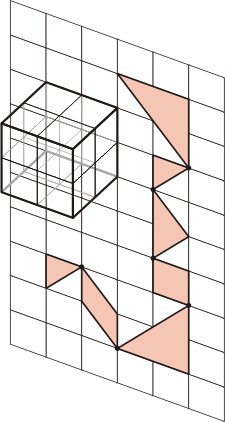 |
The Tangram Packing by Peter Grabarchuk. |
|
|
|
Tangram Packing6 |
|
This puzzle was developed by my
younger son,
Peter. The 2x2x2 cube shown in the
illustration consists of nine 2x2 square planes
intersected to produce a kind of a 3D cubic grid. Also,
you are provided with a chain of seven Tangram pieces as
shown in the illustration. The pieces in the chain are
connected with each other with joints which allow the
pieces mutually rotate and swing. The object is to put
this chain into the cube in such a way that it produces
a loop. In other words, the small triangle on the
chain's end must touch with its corner to a corner of the big triangle on
the opposite end of the chain. No two
pieces can touch each other more than in one point;
these points are the six joints, and a point of contact
for two triangles on the ends of the chain. The pieces have to be placed within the
nine planes only, thus the joints can be in the planes'
intersections. |
|
|
|
|
|
|
|
|
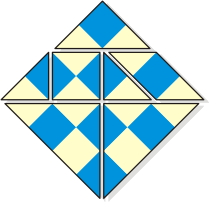
TanFrames: Squaring7 |
It's a puzzle created by my elder
son,
Serhiy Jr. In a "standard" Tangram square we can
recognize two square outlines (they're shown in green);
see the left diagram below. If we place a small square
piece next to the big square, as shown in the right
diagram, then we can see three square outlines. The
object is to place all the seven Tangram pieces so that
to form as many square outlines as possible. Each of these
outlines must be fully closed. Pieces can be rotated and
flipped over, but not overlapped.
This puzzle has several different solutions, but finding
even one of them is quite difficult, and very pleasant
task. Also, there is still a question whether it is
possible to form seven square outlines.
|
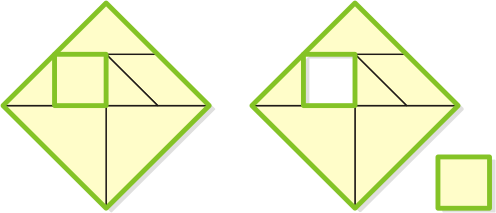 
|
Square outlines formed with
the TanFrames by Serhiy Grabarchuk, Jr.
|
|
|
|
Uniline Tangram: T-Unicursal8 |
Another puzzle developed by my
younger son,
Peter. Using all the seven pieces of the classic Tangram,
form the T-shape shown below right. The shape must be
assembled so that its whole pattern created with all the
pieces' outlines is unicursal. This means that you
should be able to drawn it in one continuous, open-ended
line which doesn't cross itself. The pieces can be
rotated and flipped over, but not overlapped. Note that
when pieces touch each other along their edges they form
a single line.
|
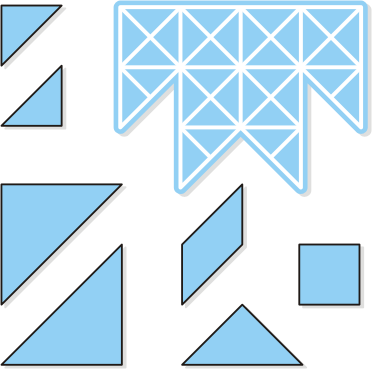 
|
Uniline Tangram: T-Unicursal by Peter
Grabarchuk.
Using all the seven pieces, form the unicursal T-shape.
|
|
|
|
Theme E: Skew vs Rectangular |
|
|
|
The Diamond Puzzle9 |
It's an old puzzle that was used
some more than a century ago for advertising purposes by
the soup and sauce manufacturer T. A. Snider Preserve
Co. with pictures of their products on the puzzle
pieces. (I'm grateful to Will Shortz that he found for
me a sample of this rare puzzle). Also, a wooden version
of this puzzle was produced in Japan under the name
"Parallel."
|
 
|
Ten pieces of the T. A.
Snider Diamond Puzzle.
|
 |
Package of the T. A. Snider Diamond Puzzle. |
|
|
|
The puzzle consists of ten skew
pieces, which can form six equal parallelograms as
shown above; the pieces are one-sided. Thus you can easily
put the whole set into the parallelogram package shown
at left. In all of its versions the puzzle was always
given with a single challenge -- to form a perfect(!)
plain square. Can you find out how it can be done? |
|
|
|
Recently, I've discovered many new
challenging shapes to the puzzle. It was a big surprise
that among these shapes there are two more exactly
rectangular ones: a normal rectangle with its length
longer than its width, and a rectangular frame -- a
rectangle with a rectangular hole in it! First these two
shapes were presented at the
Puzzles.COM
website. These two rectangular shapes along with two
more ones are shown below; try to form them all. Moreover, there
is a subset of four pieces which can make a perfect
square of smaller sizes. Can you see it? Keep in mind
that all the ten pieces are one-sided, and they
can be rotated, but not flipped over or overlapped.
|
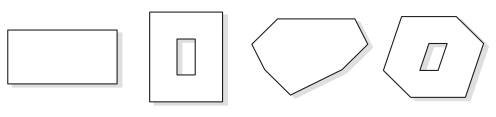
|
Some shapes assembled using
all the ten pieces of the T. A. Snider Diamond Puzzle.
|
Also, a surprisingly rich task is
to form of all the ten pieces different convex polygons.
Besides several convex triangles and quadrangles, there
are convex pentagons, hexagons, heptagons, and octagons.
Two heptagons are shown below. Perhaps, there are convex enneagons and decagons as well. Generally, it is not too
easy challenge, partially, because the pieces are
one-sided. The main question is: How many convex
polygons can be formed at all? It remains open.
|

|
Two convex heptagons
assembled using all the ten pieces of the T. A. Snider
Diamond Puzzle.
|
|
Martin Gardner in his Second
Scientific American Book of Mathematical Puzzles and
Diversions (1961),10
describes a similar task for the seven pieces of the
classic Tangram puzzle solved in 1942 by Fu Traing Wang
and Chuan-Chih Hsiung.11 There are exactly thirteen
convex polygons formed with all the seven Tangram
pieces, if to allow flipping over a parallelogram piece.
All these convex Tangram shapes are also shown in Martin
Gardner's book, Time Travel and Other Mathematical
Bewilderments (1988),12 but certainly you can enjoy finding
them all on your own. |
|
|
|
|
|
Theme F: The Rich Vintage Puzzle |
|
|
|
Martha's Vineyard |
|
This is an optimization puzzle. The
challenge is to plant a square vineyard that has a side
of 52 feet and 2 inches with the maximum of grape vines
placed no closer than nine feet apart. In his
Cyclopedia, Loyd shows a solution with 41 vines. Also,
in the book another solution with a 60-degree
array is shown, but there was a mistake or inaccuracy in that
60-degree diagram, and that's why the solution it
presents was wrong, although, in fact, this diagram
could produce a solution even better than with 41 vines. |
 |
The “Martha’s Vineyard”
puzzle as it appeared in Loyd’s
Cyclopedia of 5000 Puzzles, Tricks & Conundrums.
|
Some years ago this puzzle was
posed as a part of a Ukrainian puzzle championship, and
it brought a lot of improved solutions, which allow to
plant up to 46(!) grape vines. Two solutions with 41 and 42
vines, respectively, are shown below. Try to find
solutions with 43, 44, 45, or 46 vines on your own. The
latter one with 46 vines is very unusual and elegant.
|

|
Two solutions to Loyd’s
“Martha’s Vineyard” puzzle: 41 and 42 vines, respectively.
|
|
|
|
Theme G: Centuries of the Ovals |
|
|
|
The Two Ovals-to-Table Story13 |
This is a well-known dissection
puzzle with the object to transform two oval stools into
a circular table top. The comprehensive story about it
can be found in
Greg Frederickson's
book,
Dissections: Plane & Fancy,
published in 1997. Chapter 15 in that book is fully
devoted to dissections with curved figures, and also
describes the puzzle with two hollow ovals and some
other variations of it. More than 180 years ago, in
1821, John Jackson posed this puzzle in his book
Rational Amusement for Winter Evenings, and proposed an
8-piece solution. Can you find it?
|
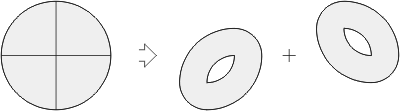 
|
Jackson’s Table & Oval
Stools puzzle.
|
Then, at the beginning of the 20th
century, this puzzle attracted attention of Sam Loyd. He
showed a better, 6-piece solution which was based on a
famous Great Chinese Monad pattern. In his book, Greg
Frederickson shows quite different, novel 6-piece
solution to Jackson's ovals. Try to find any of the 6-piece
solutions.
|
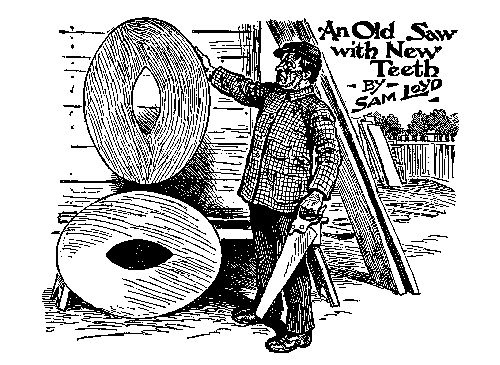 |
Loyd's "An Old Saw with New Teeth" puzzle as it appeared
in his Cyclopedia of 5000 Puzzles, Tricks &
Conundrums.
|
|
|
In March of 2004, I was lucky to
discover several new 6-piece solutions, two basic
solutions containing just five(!) pieces each, more than
a dozen of different modifications of these basic
5-piece solutions, and the proofs that in math sense there
is an infinite number of 5-piece solutions. In every of
them one piece is flipped over. Could you discover how
it can be done?
Finding any of the 6- or 5-piece solutions is rather a hard
task, so adding some grids to the puzzle shapes is
always very helpful. As hints you may use the specially
patterned diagrams shown below. Keep in mind that these diagrams
contain all necessary lines to make your cuts, but not
every of the diagrams' lines you will need to use, though.
|
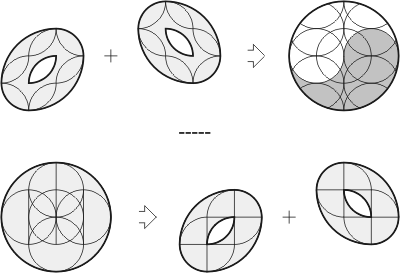 
|
Two diagrams with hint
patterns for finding 6- and 5-piece solutions to
Jackson’s Table & Oval Stools puzzle.
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
Last
Updated: December 3, 2009
Posted: May 28, 2006 |
|
|
|
|
|
|
|
|
|
